in English | suomeksi about – lectures – models – simulation – report151 – publications – links – guestbook

Background Information: A Case Example of Neurons

Studies on neocybernetics suggest that the adaptive mechanism of cybernetic models and thus the properties of the illustrated emergent systems may be ubiquitous in nature. As an example, consider neurons, 10–100 billion of which compose the human nervous system:

Neurons typically have one axon for signaling action potentials and several (e.g. 5 000 or even 150 000) synaptic connections via their dendrites to bring signals and their higher combinatorics from other neurons’ axons. Action potentials of a neuron can be recorded as time series:

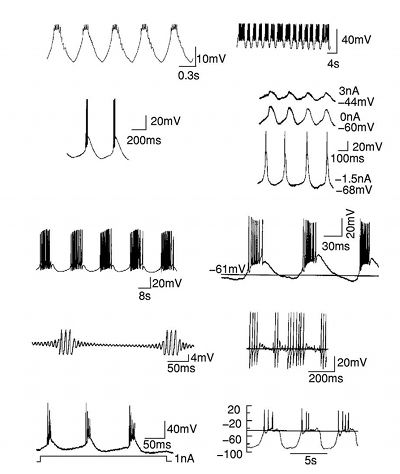
One way to model neuronal activity is to integral transform action potentials into time-frequency space where the strongest frequency (time-average of pulses in an interval) or a distribution of different frequencies serve as real-valued (or complex-valued with phase) tensions that the synapse between two neurons experiences as pre-synaptic (uj) and post-synaptic (xi) activity.

 

To get insight on the functioning of a single synapse, consider Donald O. Hebb (1949):

When an axon of cell A is near enough to excite cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A’s efficiency, as one of the cells firing B, is increased.

A common way to formalize this empirical observation is to assume that the simplest but still usable model of a synapse is a linear function on the input signal. Then the Hebbian learning can be characterized as adapting the synapse strength locally to match the covariance 𝔼{xiuj} – i.e. neurons that fire together, wire together.

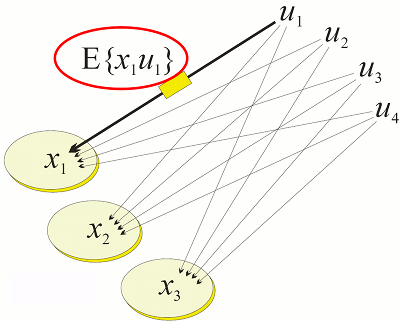
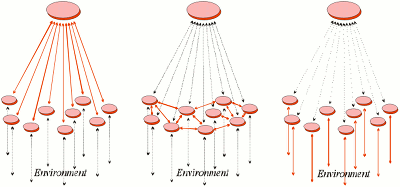
Granularizing away neurochemical details such as short-term and long-term potentiation and depression, a single neuron can thus be modeled as a synaptic weight profile vector in a resource space, the stochastic distribution of which is assumed stationary. Then in a hypothetical dynamic balance the current neuron activity xi is simply the vector inner product of the synaptic weight model vector phii and the current input resource vector u. When multiple neurons experience partly the same resource space (are connected to same neuronal populations), the models of multiple neurons or neuron groups can be combined into a single matrix phi, possibly weighted with neuron specific coupling factors qi. This results in the neocybernetic models illustrated above.

To balance the models without postulating centralized control the neurons can be augmented with lateral inhibitory connections or even more simply by assuming that even the pre-synaptic resource environment serves as a crude communicative medium when separate neurons connected to the same axon diminish the excitatory action potentials according to their synaptic profiles – i.e. exploitation means exhaustion.

In addition, the importance of sparse representations in nature have been noticed in recent decades:

Several theoretical, computational, and experimental studies suggest that neurons encode sensory information using a small number of active neurons at any given point in time. This strategy, referred to as “sparse coding”, could possibly confer several advantages. First, it allows for increased storage capacity in associative memories; second, it makes the structure in natural signals explicit; third, it represents complex data in a way that is easier to read out at subsequent levels of processing; and fourth, it saves energy. Recent physiological recordings from sensory neurons have indicated that sparse coding could be a ubiquitous strategy employed in several different modalities across different organisms. (Olshausen, Bruno A., and David J. Field. 2004. Sparse coding of sensory inputs. Current Opinion in Neurobiology: 481–487.)

The neocybernetic strategy implicitly penalizes model size, and this can be further boosted by allowing only positive activations, cutting negative inner products to zero. This results in sparse representations, where only a few neurons (models as distributed system components) are active for a given resource sample.

Neocybernetic Hypothesis

The resulting functional scheme involving implicit feedback is simple and feasible in different phenospheres. Here the structure is represented in terms of early 20th century theoretical biologist Jakob von Uexküll and augmented with the concept of monads, used by Gottfried Leibniz (1646—1716) among others.

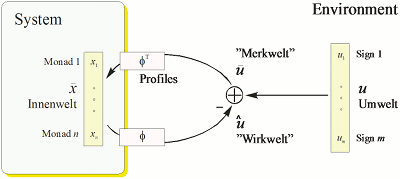
As an example of related natural philosophical thinking, philosopher Nicholas Rescher articulates monadology or monads as follows:

The principal standard bearer of process theory in modern philosophy was Leibniz, who maintained that all of the “things” that figure in our experience, organisms alone excepted, are mere phenomena and not really unified substances at all. The world, in fact, consists of clusters of minute, virtually punctiform processes he called monads (units), which are “centers of force”—in fact, bundles of activity. These monads aggregate together to make up and constitute the world’s things as we experience them. But each individual monad is a unit unto itself—an integrated whole of programmed change that denominates it as a single, unified, long-term process.
Although Leibniz is often miscast as a “pluralist”—the exponent of an ontology of many substances—the fact remains that he contemplated only one type of “substance” in nature, the monads, which actually are nothing but pure processes. Each of these monads is endowed with an inner drive, an “appetition” which ongoingly destabilizes it and provides for a processual course of never-ending change. The whole world is one vast systemic complex of such active processual units. They are programmed agents—“incorporeal automata“— developing in coordinated unison as individual centers of activity operating at different levels of sophistication within an all-comprising unified cosmic whole. Even as a differential equation generates a curve that flows over a mathematical surface, so the internally programmed dynamism of a monad leads it to unfold naturally over the course of time, tracing out its life history from beginning to end. Leibniz accordingly viewed the world as is [sic] an infinite collection of agents (monads) linked to one another in an all-pervasive harmony, with each agent, like a member of an orchestra, playing its part in engendering nature’s performance as a whole. On this basis, Leibniz developed a complex theory of nature as an integrated assemblage of harmoniously coordinated eventuations so that processes, rather than substantial objects, furnish the basic materials of his ontology.
(Process Metaphysics: An Introduction to Process Philosophy, 1996, pp. 12–13. See also the entry on process philosophy in the Stanford Encyclopedia of Philosophy.)

When the structure of the apparently simple neocybernetic system is examined closer, the models can be proven to determine an algebraic loop between the resource space and the system activities. The local adaptive mechanism of models (match components to 𝔼{xiuj}) actually results in the emergent system implementing regularized principal subspace regression from the resource space back to itself. This is a remarkable discovery – the optimality of the local strategy justifies the hypothesis that cybernetic models may well be ubiquitous in nature:

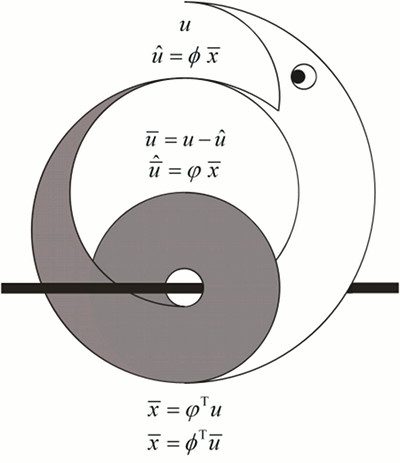
As the system is essentially linear, it can be analyzed further than most neural network algorithms. For example, the largest eigenvalues of resource space covariance matrix are attenuated according to models' coupling coefficients qi:

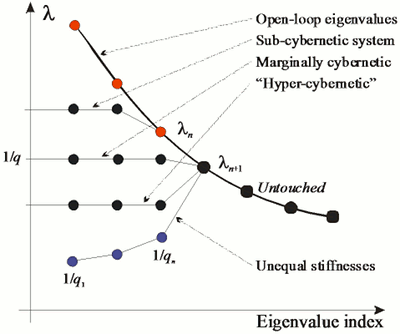
As the variation in resource space is partially transformed into model activities, the resource space becomes stiffer:

There is actually a threshold coupling level below which the model will not get excitation at all, so it seems natural that coupling levels tend to increase. Moreover, there is an optimal coupling level above which the model activation will diminish in a given resource space distribution.

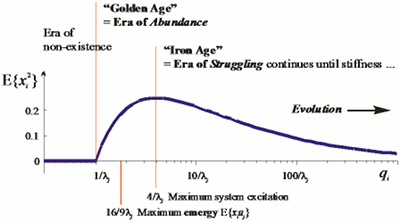
From a cybernetic point of view this may give new insight into problems that have been called is-ought-problem, fact-value distinction, naturalistic fallacy, among others. As far as a model or an emergent system of models is concerned, something may be said about how things should be, based on how they are: relevant degrees of freedom must be found, otherwise the model or a system that is dependent on them will not exist soon – finding new degrees of freedom and utilizing them are possibly intrinsically valued.