Emergentit lineaariset mallit

Johdanto

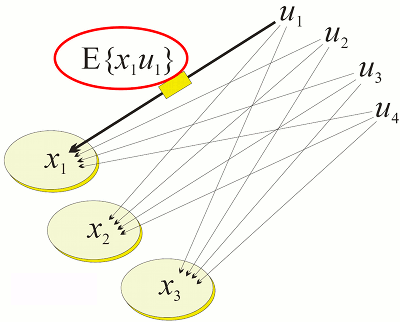
Tämä simulaatio havainnollistaa datan dynaamisia tasapainopiirteitä, emergenttejä lineaarisia malleja, moniulotteisessa resurssiavaruudessa. Esityksen yksinkertaistamiseksi vain parikymmentä pienidimensioista resurssinäytettä edustavat monimutkaista ympäristöä. Mallit määrittävät prosessit joiden avulla voidaan esittää ja arvioida emergenttejä resurssitihentymiä, kyberneettisiä tasapainoja. Simulaatio perustuu neokyberneettisiin järjestelmiin jossa systeemin aktiivisuudet x_i ovat lineaarisia (ja mahdollisesti harvoja, sparse) tasapainottavia muunnoksia resurssien residuaaleista ū ja malleja phi_i mukautetaan kohti paikallista keskinäisen kyberneettisen informaation täsmäämistä . Toisin sanoen systeemin aktiivisuus on muuttuvien ulkoisten kenttien herättämien termostaattivasteiden superpositio. Vasteet ovat kytköksissä efektiivisiin kenttiin vasteiden superpositioiden ja efektiivisten kenttien välisten emergenttien (keskiarvoisten) vuorovaikutusten moduloimina.

Simulaatio osoittaa kuinka tämä paikallinen toimintaperiaate johtaa emergentteihin järjestelmätason ominaisuuksiin kuten:

Joustava kestävyys. Järjestelmä vastaa toiminnallisella diffuusiolla palauttaakseen dynaamisen tasapainon.
Mukautuva sitkeys ja emergentit mallit. Mallivektorit suuntautuvat virittämään resurssijakauman pääaliavaruuden (principal subspace), heijastaen olennaisia hahmoja ja suodattaen kohinaa.
Optimaalinen vakavointi. Moniulotteinen resurssiavaruus vaimenee luontaisen mallipohjaisen säädön johdosta, kun resurssiherätettä kulutetaan osittain systeemin toimintaan.

Aluksi vain kaksiulotteinen kyberneettinen systeemi mallivektoreineen (sininen ja ruskea) kaksiulotteisten resurssinäytteiden (vaaleat pisteet) ajamana on esillä. Resurssinäytteet vaimenevat (vaaleat viivat) luontaisen resurssien käytön johdosta, mikä antaa arvion (musta ympyrä) tämänhetkisestä resurssista (mustat kiekot hiiren kohdalla). Emergentit lineaariset mallit vaikuttavat toisiinsa vain resurssiympäristön välityksellä, mutta virittävät kokonaisuutena toiminnallisesti mielenkiintoisen rakenteen. Katso ”controls”-välilehteä ja demon alla olevia animaatioita oppiaksesi lisää.

Tutki vuorovaikutteista demoa

Korkeampiulotteisia esimerkkejä

Simulaatio esittää vain 1–5-ulotteisen systeemin 2–5-ulotteisessa resurssiavaruudessa. Käyttökelpoisia tuloksia saadaan korkeampiulotteisissa avaruuksissa. Avaruudet voivat koostua mistä vain äärellisestä datasta (esimerkiksi lisättynä viivästetyillä, yhdistetyillä tai muulla tavoin muunnetuilla resursseilla), mutta kenties havainnollisinta on esittää muutama esimerkki joissa avaruuden rakenne on intuitiivisesti selvä: kuvien käyttö moniulotteisina resursseina. Kukin alla olevista esimerkeistä on alustettu satunnaisilla mallivektoreilla resurssiavaruudessa joka on kuvadatan määrittämä.

Numerot A – 10-ulotteinen systeemi 256-ulotteisessa resurssiavaruudessa 500 resurssinäytteellä. Resurssinäytteet ovat käsinkirjoitettuja numeroita esitettyinä 16×16=256-ulotteisina vektoreina. Mallivektorit näyttävät suuntautuvan esittämään resurssiavaruuden kasaantumia.
Numerot B – 40-ulotteinen systeemi 256-ulotteisessa avaruudessa 500 näytteellä. Resurssinäytteet ovat samoja käsinkirjoitettuja numeroita kuin yllä. Näyte (alla toinen oikealta) voidaan rakentaa (alla oikealla) lisäämällä yhteen aktiiviset mallivektorit. Vain muutamat mallivektorit ovat aktiivisia kullakin resurssinäytteellä (aktiivisuutta ei esitetä animaatiossa), ja eri mallivektoreita voidaan jakaa eri esitysten kesken – hajautettu koodi on harva ja eri mallivektorit pyrkivät vastaamaan erilaisiin viivoihin.
Kasvot – 30-ulotteinen systeemi 560-ulotteisessa avaruudessa 1965 näytteellä. Resurssinäyte (alla vasemmalla) voidaan rakentaa (alla oikealla) ilmeitä esittävien aktiivisten mallivektorien lineaarikombinaationa (30 lähes kohtisuoraa vektoria, kukin 28×20=560-ulotteinen).
Numerot C – 100-ulotteinen agenttisysteemi 1024-ulotteisessa avaruudessa 8940 näytteellä. Näytteet ovat käsinkirjoitettuja numeroita esitettyinä 32×32=1024-ulotteisina vektoreina. Tällä kertaa kytkentämatriisissa Q on nollasta poikkeavia positiivisia arvoja myös muualla kuin diagonaalilla, joten mallivektorit vastaavat myös lähinaapureihinsa tasossa.
Numerot D – 100-ulotteinen agenttisysteemi 1024- ja 10-ulotteisissa avaruuksissa 8940 näytteellä. Näytteet ovat samoja käsinkirjoitettuja numeroita kuin edellisessä tapauksessa. Ei-diagonaalisen kytkentämatriisin Q lisäksi tässä hyödynnetään myös luokkanimikkeitä: 10-ulotteinen rinnakkainen resurssiavaruus osoittaa mikä kukin luku on (0–9), ja systeemi vastaa samanaikaisesti kumpaankin avaruuteen. Siten mallivektorit heijastavat myös lisämääreiden välittämää informaatiota eivätkä ainoastaan yhden resurssiavaruuden rakennetta. Tuloksia voidaan käyttää esimerkiksi Partial Least Squares (PLS) / Canonical Correlation Analysis (CCA) -tyypiseen aliavaruusregressioon – hajautettuna, regularisoituna ja harvakoodattuna.

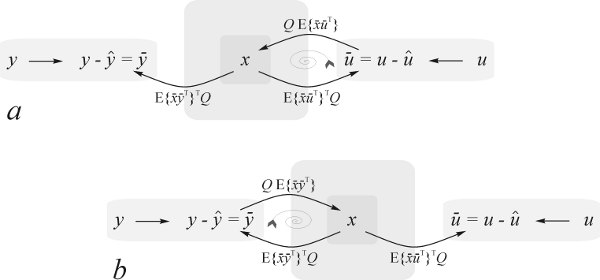
Lisäksi uusimpia kehityksiä ovat olleet kompleksilukujen käyttö algoritmeissa, jolloin vaiheen avulla voidaan mallittaa myös muutosjännitteet samassa viitekehyksessä.

Uutta: voit kokeilla algoritmia R-ympäristössä: eca.r. Perinpohjaisempi opastus jää myöhemmäksi. Sillä välin luennot kybernetiikan alkeista, erityisesti 4. luento ja sitä seuraavat, käsittelevät mallia, ja on myös tarjolla joitakin yhteenvetoja ja tarkempia analyyseja.

Sovelluksia

Neokybernetiikka voi tarjota uusia mahdollisuuksia kompleksisten järjestelmien tutkimukseen ja kehitykseen, mm. bioinspiroituneen ja hyperulotteisen laskennan saralla. Katso luentoja ja julkaisuja toisaalla tällä sivustolla, esimerkkejä:

Tilastollisia menetelmiä sovellettuna ohjelmallisiin antureihin, antureiden yhdistelyyn ja kalibrointiin
Emergenttejä toimintamalleja sovellettuna teollisuuslaitosten asetusarvojen optimointiin
”Fraktaalisen häiriönsiedon” ajatusta sovellettuna voimalaitosverkoston uudelleensuunnitteluun ja analyysiin

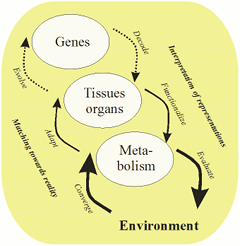
Systeemibiologia, geneettisten ja aineenvaihdunnan järjestelmien mallintamista dynaamisilla malleilla
Luonnon monimuotoisuus ekosysteemeissä ja talousjärjestelmissä, ja niiden laadullisen käyttäytymisen arviointia
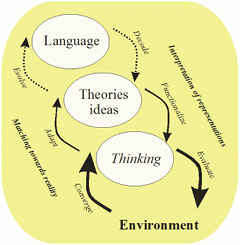
Rakenteellisia malleja hermostollisille ja kognitiivisille järjestelmille, ja uusia kieliä niille

Laadullisten ja laskennallisten menetelmien risteyttämistä ihmistieteissä, kuten käyttäytymis- ja yhteiskuntatieteissä
Systeemiteoreettisia kontribuutioita (matemaattiseen) luonnonfilosofiaan

Neokyberneettinen ehdotus

Yhteenvetona, neokybernetiikan tutkimukset antavat ymmärtää että lähes kaikki on informaatiota (yhteisvaihtelua, kovariaatiota) – havaittujen pysyvien rakenteiden perusolemus koostuisi resurssiavaruuden kuvausten ja entropian tavoittelun määräämistä dynaamisten prosessien tasapainopiirteistä. Elämää voisi siten luonnehtia – tavanomaisempaa iturataa yleisemmin – pyrkimykseksi kohti fraktaalista toimintojen tasapainoa monenlaisissa ympäristöissä.