in English | suomeksi neokybernetiikasta – luentoja – mallit – simulaatio – tutkimusraportti – julkaisuja – linkkikokoelma – vieraskirja

Taustaa: hermosolujen tapausesimerkki

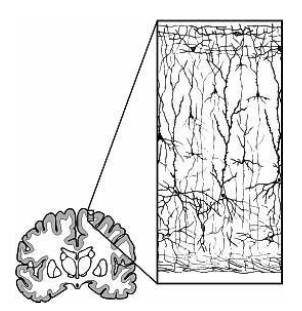
Neokybernetiikan tutkimukset viittavat siihen, että kyberneettisten kytkentöjen mukautuva mekanismi ja siten esitettyjen emergenttien lineaaristen mallien ominaisuudet saattavat olla läsnä kaikkialla luonnossa. Esimerkkinä tarkastellaan hermosoluja, joista ihmisen hermosto (10–100 miljardia hermosolua) koostuu:

Hermosoluilla on yleensä yksi viejähaarake (aksoni) aktiopotentiaalien signalointiin ja useita synaptisia yhteyksiä (esim. 5 000 tai jopa 150 000) tuojahaarakkeissaan (dendriitit) joiden kautta signaaleja ja niiden kombinaatioita saapuu muiden hermosolujen aksoneista. Hermosolujen aktiopotentiaaleja voidaan mitata aikasarjoina:

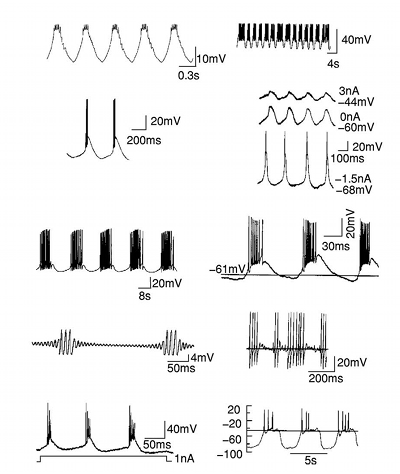
Yksi tapa mallittaa hermosolun toimintaa on integraalimuuntaa aktiopotentiaalit aika-taajuus -avaruuteen jossa voimakkain taajuus (sykäysten aikakeskiarvo jollain välillä) tai eri taajuuksien jakauma muodostaa reaaliarvoisia (tai kompleksiarvoisia vaiheineen) jännitteitä jotka kahden hermosolun välillä oleva synapsi kokee esisynaptisena (uj) ja jälkisynaptisena (xi) toimintana.

 

Saadakseen näkemystä yksittäisen synapsin toimintaan, voi pohtia Donald O. Hebbin kirjoittamaa (1949):

Kun solun A viejähaarake on tarpeeksi lähellä vaikuttaakseen soluun B ja toistuvasti tai alituisesti ottaa osaa sen laukaisemiseen, jokin kasvuprosessi tai aineenvaihdunnan muutos tapahtuu toisessa tai kummassakin solussa, siten että A:n vaikuttavuus, yhtenä B:tä laukovana soluna, voimistuu.

Yleinen tapa formalisoida tämä kokeellinen havainto on olettaa että yksinkertaisin mutta silti käyttökelpoinen malli synapsille on syöttösignaalin lineaarinen funktio. Silloin Hebbiläistä oppimista voidaan luonnehtia synapsin vahvuuden paikallisena muokkautumisena kovarianssin 𝔼{xiuj} mukaan – eli hermosolut jotka laukovat yhdessä, kytkeytyvät yhteen.

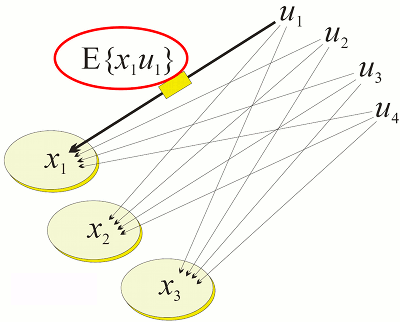
Karkeistaen neurokemialliset yksityiskohdat kuten lyhyen ja pitkän aikavälin kohoamat ja alenemat (short-term and long-term potentiation and depression), yksittäinen hermosolu voidaan siis mallittaa synaptisten painojen mallivektorina resurssiavaruudessa jonka tilastollinen jakauma oletetaan muuttumattomaksi. Silloin hypoteettisessa dynaamisessa tasapainossa sen hetkinen hermosolun aktiivisuus xi on yksinkertaisesti synaptisten painojen mallivektorin phii ja sen hetkisen syöttävän resurssivektorin u sisätulo. Kun useat hermosolut kokevat osittain saman resurssiavaruuden (ovat kytkeytyneet samoihin neuronipopulaatioihin), eri hermosolujen tai hermosolujoukkojen mallivektorit voidaan yhdistää yhteen matriisiin phi, mahdollisesti painotettuina hermosolukohtaisilla kytkentäkertoimilla qi. Tämä johtaa yllä esitettyyn neokyberneettiseen malliin.

Malli voidaan tasapainottaa olettamatta keskitettyä ohjausta jos hermosolujen välille lisätään poikittaisia estäviä yhteyksiä, tai vielä yksinkertaisemmin olettamalla että jopa esisynaptinen jresurssiympäristö voi toimia karkeana viestintäkanavana jos samaan aksoniin kytkeytyneet eri neuronit heikentävät herättäviä aktiopotentiaaleja synaptisten mallivektoriensa mukaan – eli käyttäminen merkitsee myös kuluttamista.

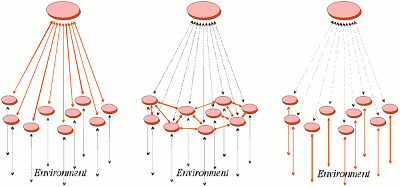
Lisäksi harvojen kuvausten (sparse representations) tärkeys luonnossa on huomattu viime vuosikymmeninä:

Useat teoreettiset, laskennalliset ja kokeelliset tutkimukset esittävät, että hermosolut muuntavat aisti-informaation käyttäen pientä määrää aktiivisia hermosoluja kullakin ajan hetkellä. Tämä toimintaperiaate, jota kutsutaan ”harvakoodaamiseksi”, voi mahdollisesti antaa useita etuja. Ensiksi, se jättää sijaa suuremmallle tallennuskyvylle mielleyhtymämuisteihin; toiseksi, se tuo luonnollisten signaalien rakenteen selkeästi esiin; kolmanneksi, se esittää monimutkaisen datan tavalla joka on helpompi lukea myöhemmillä käsittelyn tasoilla; ja neljänneksi, se säästää energiaa. Viimeaikaiset fysiologiset tallenteet aistineuroneista ovat osoittaneet että harvakoodaus saattaa olla kaikkialla läsnä oleva toimintatapa jota useat eri organismit käyttävät eri kanavissaan (modaliteeteissa). (Olshausen, Bruno A., and David J. Field. 2004. Sparse coding of sensory inputs. Current Opinion in Neurobiology: 481–487.)

Neokyberneettinen strategia rokottaa implisiittisesti mallin kokoa, ja tätä voidaan vahvistaa edelleen sallimalla vain positiiviset aktivaatiot leikkaamalla negatiiviset sisätulot nollaksi. Tämä johtaa harvoihin kuvauksiin, joissa vain muutama hermosolu (mallivektorit hajautettuina mallin osina) on aktiivinen kullekin resurssinäytteelle.

Neokyberneettinen hypoteesi

Yllä olevasta seuraava toiminnallinen kaavio, jossa on mukana luontainen takaisinkytkentä, on yksinkertainen ja mahdollinen erilaisissa ilmiömaailmoissa. Tässä rakenne on esitetty 1900-luvun alun teoreettisen biologin Jakob von Uexküll:n sanoin, lisättynä monadien käsitteellä, jota käytti Gottfried Leibniz (1646—1716) muiden muassa.

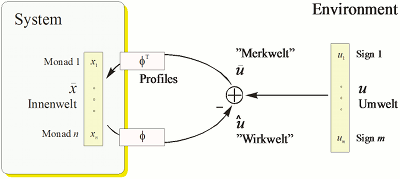
Esimerkkinä tähän liittyvästä luonnonfilosofisesta ajattelusta filosofi Nicholas Rescher kuvailee monadologiaa tai monadeja seuraavasti:

The principal standard bearer of process theory in modern philosophy was Leibniz, who maintained that all of the “things” that figure in our experience, organisms alone excepted, are mere phenomena and not really unified substances at all. The world, in fact, consists of clusters of minute, virtually punctiform processes he called monads (units), which are “centers of force”—in fact, bundles of activity. These monads aggregate together to make up and constitute the world’s things as we experience them. But each individual monad is a unit unto itself—an integrated whole of programmed change that denominates it as a single, unified, long-term process.
Although Leibniz is often miscast as a “pluralist”—the exponent of an ontology of many substances—the fact remains that he contemplated only one type of “substance” in nature, the monads, which actually are nothing but pure processes. Each of these monads is endowed with an inner drive, an “appetition” which ongoingly destabilizes it and provides for a processual course of never-ending change. The whole world is one vast systemic complex of such active processual units. They are programmed agents—“incorporeal automata“— developing in coordinated unison as individual centers of activity operating at different levels of sophistication within an all-comprising unified cosmic whole. Even as a differential equation generates a curve that flows over a mathematical surface, so the internally programmed dynamism of a monad leads it to unfold naturally over the course of time, tracing out its life history from beginning to end. Leibniz accordingly viewed the world as is [sic] an infinite collection of agents (monads) linked to one another in an all-pervasive harmony, with each agent, like a member of an orchestra, playing its part in engendering nature’s performance as a whole. On this basis, Leibniz developed a complex theory of nature as an integrated assemblage of harmoniously coordinated eventuations so that processes, rather than substantial objects, furnish the basic materials of his ontology.
(Process Metaphysics: An Introduction to Process Philosophy, 1996, pp. 12–13. See also the entry on process philosophy in the Stanford Encyclopedia of Philosophy.)

Kun ilmeisen yksinkertaisen neokyberneettisen mallin rakennetta tutkitaan lähemmin, mallivektorien voidaan osoittaa määrittävän algebrallisen silmukan resurssiavaruuden ja systeemin aktiivisuuksien välille. Mallivektorien paikallinen mukautuva mekanismi (sovita mallivektorien komponentit täsmäämään 𝔼{xiuj}) johtaakin siihen, että emergentti järjestelmä toteuttaa regularisoidun pääaliavaruusregression (principal subspace regression) resurssiavaruudesta takaisin resurssiavaruuteen. Tämä on merkittävä löytö – paikallisen toimintatavan optimaalisuus oikeuttaa hypoteesin että malli saattaa tosiaankin olla läsnä kaikkialla luonnossa:

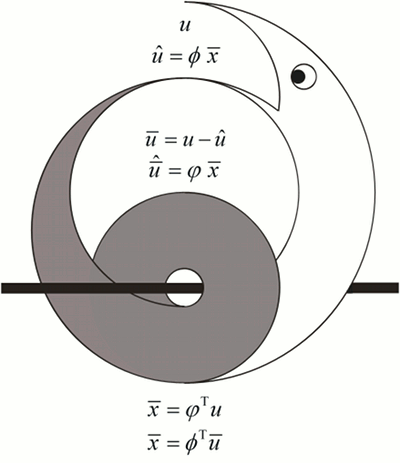
Kun järjestelmä on olennaisilta osin lineaarinen, sitä voidaan tarkastella edemmäs kuin useimpia neuroverkkoalgoritmeja. Esimerkiksi, resurssiavaruuden kovarianssimatriisin suurimmat ominaisarvot vaimenevat mallivektorien kytkentäkertoimien qi mukaan:

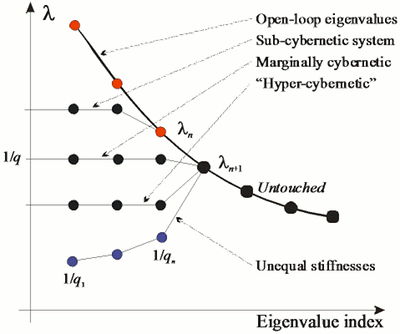
Kun resurssiavaruuden vaihtelu muuntuu osittain systeemin toiminnaksi, resurssiavaruus tulee jäykemmäksi:

Itse asiassa havaitaan että kytkentäkertoimelle on olemassa kynnysarvo jota heikommalla kytkennällä systeemi ei tule aktivoitumaan lainkaan, joten olisi luontevaa että kytkentäkertoimet pyrkivät kasvamaan. Lisäksi on olemassa optimaalinen kytkentävoimakkuus jota suuremmalla kytkennällä systeemin aktivaatio tulee vain pienenemään kyseisellä jänniteavaruuden jakaumalla.

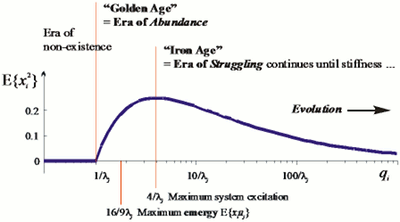
Kyberneettisestä näkökulmasta tämä voi valottaa ongelmia joita on kutsuttu on-pitäisi -ongelmaksi, tosiasioiden ja arvojen eroksi, naturalistiseksi virhepäätelmäksi, muiden muassa. Mallivektorin tai mallivektorien emergenttien kokonaisuuksien kannalta jotain voidaan sanoa siitä miten asioiden tulisi olla, sen perusteella miten ne ovat: olennaisia vapausasteita on löydyttävä, muutoin mallivektoria tai järjestelmää joka tarvitsee kyseisiä mallivektoreita ei ole pian enää olemassa – uusien vapausasteiden löytäminen ja niiden käyttäminen on mahdollisesti luontaisesti arvostettua.