Illustration of Emergent Linear Models

Introduction

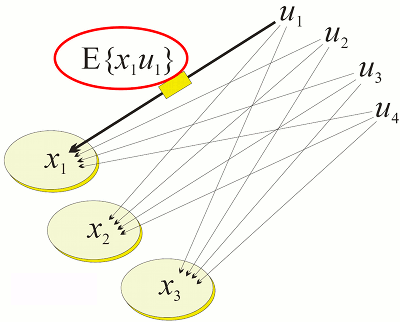
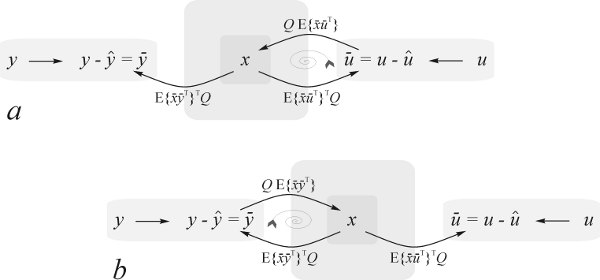
This simulation visualizes dynamic patterns, emergent linear models, of data in a multidimensional resource space. To simplify the presentation, a few dozen low-dimensional resource samples index a complex environment. The emergent models determine processes that can be used to represent and estimate resource intensities, cybernetic equilibria. The simulation is based on cybernetic systems where activities x are linear (and optionally sparse) balancing transformations of resource residuals ū and emergent models phi are adapted towards local matching of mutual cybernetic information . In other words, system activities are superpositions of dampening responses to time dependent external perturbing fields. Responses are coupled to effective fields via emergent (average) interactions between response superpositions and effective fields.

The simulation demonstrates this local strategy resulting in emergent system level properties such as:

Elastic resilience. The system reacts by generalized diffusion to restore dynamic balance.
Adaptive robustness and emergent models. The models orient themselves to span the principal subspace of the resource distribution, reflecting relevant patterns and filtering noise.
Optimal regulation. Multidimensional resource space is attenuated by implicit model-based control as resource excitation is partially consumed for system activity.

Initially only two-dimensional cybernetic system (in blue and brown) driven by two-dimensional resource samples (light dots) are shown. Resource samples are attenuated (light lines) by implicit resource use, which gives an estimate (black circle) of the current resource (black disks at mouse position). The systems interact only via their environment, but still as a whole enact functionally interesting structures. See “controls” tab and more animations below the demo to learn more.

Explore the Interactive Demo

Higher-Dimensional Examples

The simulation presents only 1–5 models in a 2–5-dimensional resource space. Useful results are obtained in higher-dimensional spaces. The spaces can be composed of any kind of finite data (for example, augmented with delayed, combined, and otherwise transformed resources), but perhaps it is most illustrative to present a few examples where the structure of the resource space is intuitively clear: using images as multidimensional resources. Each example below is initiated with random models in the resource space that is determined by image data.

Digits A – 10-dimensional system in a 256-dimensional resource space with 500 resource samples. Resource samples consist of handwritten digits presented as 16×16=256-dimensional vectors. The models seem to orient themselves to represent clusters in the resource space.
Digits B – 40-dimensional system in a 256-dimensional resource space with 500 resource samples. Resource samples consist of the same handwritten digits as above. An example resource (bottom right) can be reconstructed (bottom rightmost) by adding together active models. Only a few emergent models are active for each resource sample (activity is not visualized in the animation), and different models can be shared across representations – the distributed code is sparse and different models tend to respond to different strokes.
Faces – 30-dimensional system in a 560-dimensional resource space with 1965 resource samples. An example resource (bottom left) can be reconstructed (bottom right) by a linear combination of active models representing facial expressions (30 almost orthogonal vectors, each 28×20=560-dimensional).
Digits C – 100-dimensional agent system in a 1024-dimensional resource space with 8940 resource samples. Resource samples consist of handwritten digits presented as 32×32=1024-dimensional vectors. This time the coupling coefficient matrix Q has also non-diagonal elements so that the models respond also to their spatial, planar neighbours.
Digits D – 100-dimensional agent system in 1024- and 10-dimensional resource spaces with 8940 resource samples. Resource samples consist of the same handwritten digits as in the previous case. In addition to non-diagonal Q here also class label information is used: there is a 10-dimensional parallel resource space indexing whether the current sample is a number 0–9, and the models respond simultaneously to both spaces. Thus the models reflect also additional type information instead of only the resource space structure. The results can be used, for example, for Partial Least Squares (PLS) / Canonical Correlation Analysis (CCA) like subspace regression, in a distributed, regularized and sparse way.

In addition, among recent developments is to use complex values for representing resource magnitude and phase together, allowing modeling of resource space change tensions in the same framework.

Update: Now you can test run the algorithm in R environment for statistical computing: eca.r. A more thorough tutorial may be prepared later. In the meantime, lectures on elementary cybernetics, especially lecture 4 and later, discusses emergent linear models, and some summaries and detailed analyses are available too.

Applications

Neocybernetics may offer new possibilities for research and development of complex systems, i.a. bioinspired and hyperdimensional computing. See lectures and publications elsewhere on this site for examples on:

Statistical methods applied in soft sensors, sensor fusion, and calibration
Emergence of behaviors applied in parameter optimization of industrial systems
Idea of “fractal robustness” applied in redesign and analysis of a power plant grid

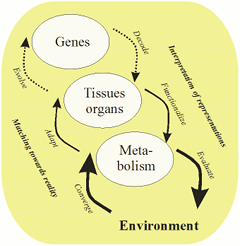
Systems biology, modeling of genetic and metabolic systems using dynamic models
Biodiversity in ecologies and economies, and estimating their qualitative behaviors
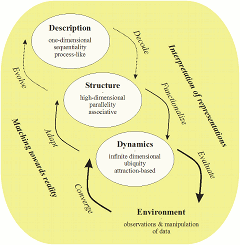
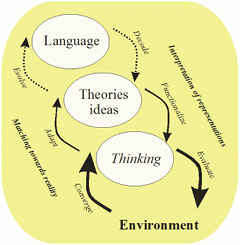
Structured models for neural and cognitive systems, and new languages for them

Crossing the boundaries of qualitative and quantitative methods in the behavioral and social sciences
Systems theoretical contributions to (mathematical) natural philosophy

Neocybernetic Proposal

As a summary, studies on neocybernetics suggest that mostly everything is information (covariation) – the essence of perceived stable structures consists of patterns of dynamic processes governed by modeling and entropy pursuit in the resource space. Life could then be characterized – in a more general way than the common understanding as the germline – as the drive towards fractal balance of functions in various environments.